Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The regions may be square or rectangular, or may have arbitrary shapes.
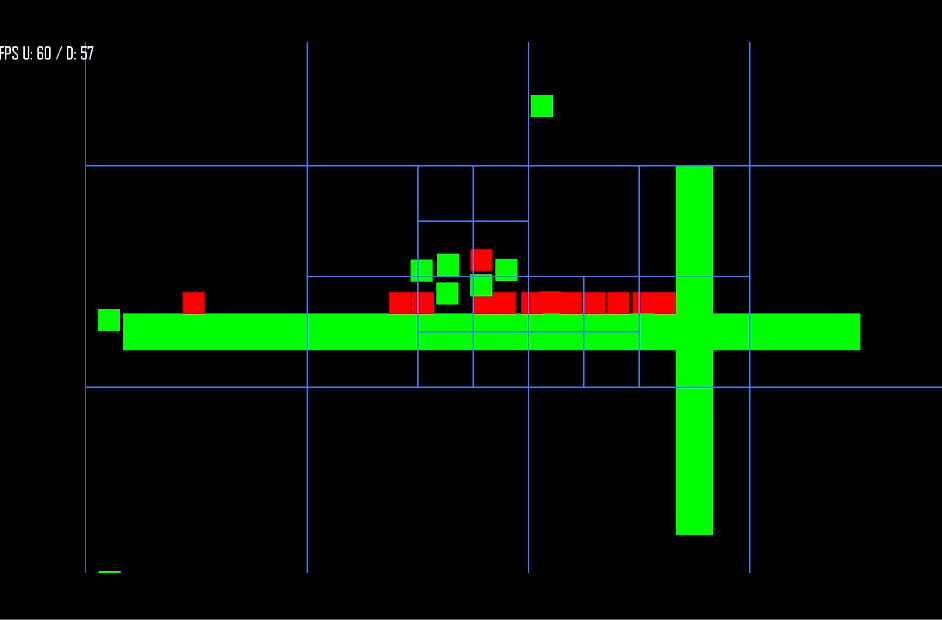
Concept
The quad tree recursively adds children to itself, other quad trees as items change coordinates. A threshold determines when a recursion should occur, splitting the region into four subregions to contain the new items.
Complexity
Theorem 1: A Quadtree of depth 'd' storing a set of 'n' points has O((d + 1)n) nodes and can be constructed in O((d + 1)n) time.
Theorem 2: Let T be a Quadtree of depth 'd'. The neighbor of a given node 'ν' in T in a given direction can be found in O(d + 1) time.
In layman's terms:
For collision detection, as an example, if I were to have 100 objects I need to check, I would normally have to compare each object to one another. This would be O(n^2) meaning that there would be 10000 check.
A Quadtree enables us to check our direct neighbors only. If it had a maximum depth of 4 created, worst case it would be O((d + 1)n) time, or O(5*100). So 500 comparisons. That's much better than 10000.
So a guaranteed 10,000 checks or a worst case 500 checks?
Areas for Improvement
If you check out the sample, one major flaw is the updating cycle of the implementation. It requires that the mobs are cleared and reinserted so that their quads are built correctly. This strategy is equivalent in complexity to updating positions of the mobs inside, simpler to understand as well. This is the main cause for pooling being built in directly.
Example Usage of Implementation
Example update loop for the object manager:
#!c++
// Update the Quadtree
quadTree.clear();
for (int i = 0; i < mobs.size(); i++)
{
quadTree.insert(mobs[i]);
}
for (int i = 0; i < mobs.size(); i++)
{
// ...
resolveCollisions(mobs[i]);
// ...
}Then within your collision resolution routine, you would need to compare the mob to its neighbors:
#!c++
virtual void resolveCollisions(Mob* _mob)
{
// ...
std::vector<Mob*> nearbyMobs;
quadTree.retrieve(&nearbyMobs, mob);
// ...
}C++ Implementation
Includes built in pooling and expects a Mob object with basic x, y, width, height etc.
#!c++
#include "Mob.h"
#include <vector>
#include <iostream>
#include <sstream>
class QuadTree
{
public:
QuadTree(int _level, float x, float y, float width, float height, int poolSize = 100)
: nodes()
{
maxObjects = 7;
maxLevels = 10;
level = _level;
bounds.left = x;
bounds.top = y;
bounds.width = width;
bounds.height = height;
shape.setPosition(x, y);
shape.setSize(sf::Vector2f(width, height));
shape.setFillColor(sf::Color(0, 0, 0, 0));
shape.setOutlineThickness(2.0f);
shape.setOutlineColor(sf::Color(64, 128, 255));
if(level == 0)
{
// The root quadtree can maintain a pool
pool = new std::vector<QuadTree*>();
for(int i = 0; i < poolSize; i ++)
{
pool->push_back(new QuadTree(-1, 0, 0, 0, 0));
}
}
}
~QuadTree()
{
if(level == 0)
{
for(int i = 0; i < pool->size(); i ++)
{
if((*pool)[i])
{
delete (*pool)[i];
}
}
delete pool;
}
for(int i = 0; i < nodes.size(); i ++)
{
if(nodes[i])
{
delete nodes[i];
}
}
}
int maxObjects;
int maxLevels;
int level;
std::vector<Mob*> objects;
sf::FloatRect bounds;
std::vector<QuadTree*>* pool;
std::vector<QuadTree*> nodes;
sf::RectangleShape shape;
/*
* Clears the quadtree
*/
void clear()
{
objects.clear();
for(int i = 0; i < nodes.size(); i++)
{
if(nodes[i])
{
nodes[i]->clear();
}
returnToPool(nodes[i]);
}
nodes.clear();
}
/*
* Splits the node into 4 subnodes
*/
void split()
{
int subWidth = (int)(bounds.width / 2);
int subHeight = (int)(bounds.height / 2);
int x = (int)bounds.left;
int y = (int)bounds.top;
nodes.push_back(fetchFromPool(level+1, x + subWidth, y, subWidth, subHeight));
nodes.push_back(fetchFromPool(level+1, x, y, subWidth, subHeight));
nodes.push_back(fetchFromPool(level+1, x, y + subHeight, subWidth, subHeight));
nodes.push_back(fetchFromPool(level+1, x + subWidth, y + subHeight, subWidth, subHeight));
}
QuadTree* fetchFromPool(int _level, float x, float y, float width, float height)
{
QuadTree* fromPool;
if(pool->size() > 0)
{
fromPool = pool->back();
pool->pop_back();
}
else
{
fromPool = new QuadTree(-1, 0, 0, 0, 0);
}
fromPool->level = _level;
fromPool->bounds.left = x;
fromPool->bounds.top = y;
fromPool->bounds.width = width;
fromPool->bounds.height = height;
fromPool->pool = pool;
return fromPool;
}
void returnToPool(QuadTree* quadTree)
{
quadTree->level = -1;
quadTree->bounds.left = 0;
quadTree->bounds.top = 0;
quadTree->bounds.width = 0;
quadTree->bounds.height = 0;
quadTree->pool = NULL;
pool->push_back(quadTree);
}
/*
* Determine which node the object belongs to. -1 means
* object cannot completely fit within a child node and is part
* of the parent node
*/
int getIndex(Mob* pRect)
{
int index = -1;
double verticalMidpoint = bounds.left + (bounds.width / 2);
double horizontalMidpoint = bounds.top + (bounds.height / 2);
// Object can completely fit within the top quadrants
bool topQuadrant = (pRect->box.top < horizontalMidpoint && pRect->box.top + pRect->box.height < horizontalMidpoint);
// Object can completely fit within the bottom quadrants
bool bottomQuadrant = (pRect->box.top > horizontalMidpoint);
// Object can completely fit within the left quadrants
if (pRect->box.left < verticalMidpoint && pRect->box.left + pRect->box.width < verticalMidpoint)
{
if (topQuadrant)
{
index = 1;
}
else if (bottomQuadrant)
{
index = 2;
}
}
// Object can completely fit within the right quadrants
else if (pRect->box.left > verticalMidpoint)
{
if (topQuadrant)
{
index = 0;
}
else if (bottomQuadrant)
{
index = 3;
}
}
return index;
}
/*
* Insert the object into the quadtree. If the node
* exceeds the capacity, it will split and add all
* objects to their corresponding nodes.
*/
void insert(Mob* pRect)
{
if (nodes.size() > 0)
{
int index = getIndex(pRect);
if (index != -1)
{
if(index < 0 || index > nodes.size())
{
bool f = false;
}
nodes[index]->insert(pRect);
return;
}
}
objects.push_back(pRect);
if (objects.size() > maxObjects && level < maxLevels)
{
if (nodes.size() == 0)
{
split();
}
int i = 0;
while (i < objects.size())
{
int index = getIndex(objects.at(i));
if (index != -1)
{
// TODO: gross clean up this
Mob* mob = objects.at(i);
objects.erase(objects.begin() + i);
nodes[index]->insert(mob);
}
else
{
i++;
}
}
}
}
/*
* Return all objects that could collide with the given object
*/
std::vector<Mob*>* retrieve(std::vector<Mob*>* returnObjects, Mob* pRect)
{
int index = getIndex(pRect);
if (index != -1 && nodes.size() > 0)
{
nodes[index]->retrieve(returnObjects, pRect);
}
for(int i = 0; i < objects.size(); i++)
{
returnObjects->push_back(objects[i]);
}
return returnObjects;
}
};