A* Pathfinding
A* Pathfinding is the premier performant pathfinding algorithm for game development. Though less accurate than Dijkstra's algorithm the speed improvements are immense. It uses a few heuristics to determine pathfinding, and attempts a straight line direction before deviation begins.
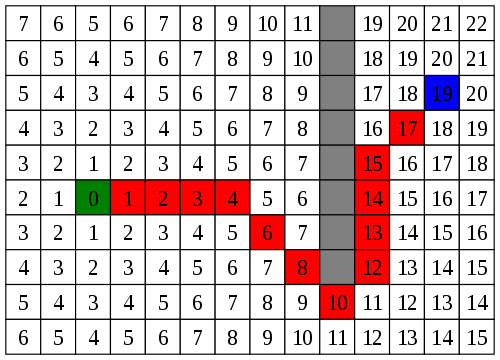
Concept
A* uses a series of closed and open identifiers to determine whether connected nodes have been traversed, are blocked, or are open. The algorithm is more or less set, but there are three key components that can be replaced to implement your game level implementation of A*.
- Node Connection - You can easily plug in your own game logic for determining what nodes are "neighbors" of other nodes.
- Blocked Nodes - You determine what nodes are considered blocked, and this can be custom to any given scenario for your game.
- Game Node Objects - You can connect any object that implements the node container interface into the algorithm to retrieve more useful paths.
Example Usage of Implementation
C++ Node Class
#ifndef NODE_H
#define NODE_H
class Node
{
public:
Node();
Node(int x, int y);
// Node Details
int x;
int y;
// A Star details
bool closed, opened;
bool isBlocked;
int fCost;
int gCost;
int hCost;
Node* aStarParent;
bool equals(Node* compareNode);
void resetAstar();
sf::Vector2f toVector2();
};
#endif
#include "Node.h"
Node::Node()
{
this->fCost = 0;
this->gCost = 0;
this->hCost = 0;
this->x = 0;
this->y = 0;
this->isBlocked = false;
this->aStarParent = NULL;
this->closed = false;
this->opened = false;
}
Node::Node(int x, int y)
{
this->fCost = 0;
this->gCost = 0;
this->hCost = 0;
this->x = x;
this->y = y;
this->isBlocked = false;
this->aStarParent = NULL;
this->closed = false;
this->opened = false;
}
bool Node::equals(Node* compareNode)
{
return (x == compareNode->x && y == compareNode->y);
}
void Node::resetAstar()
{
gCost = 0;
hCost = 0;
fCost = 0;
aStarParent = NULL;
closed = false;
opened = false;
}
sf::Vector2f Node::toVector2()
{
// ...
}C++ A* Pathfinding
std::vector<GameObject*> aStarPathfind(GameObject* startNode, GameObject* endNode)
{
std::list<GameObject*> OpenList;
std::list<GameObject*> ClosedList;
std::vector<GameObject*> path; // the shortest path
// add start node to open list
GameObject* currentNode = startNode;
ClosedList.push_back(currentNode);
currentNode->node->closed = true;
while (!currentNode->node->equals(endNode->node))
{
// Mechanism for comparing neighbors
std::vector<GameObject*> surrounding = getNeighbors(currentNode);
// Loop to look for best candidate via A*
for (int i = 0; i < surrounding.size(); i++)
{
GameObject* cNode = surrounding[i];
int xdiff;
int ydiff;
int gcost;
int hcost;
if (cNode->node->gCost == 0) // gcost
{
// this is the difference between the current node x and y and this node x and y
xdiff = std::abs(cNode->node->x - currentNode->node->x);
ydiff = std::abs(cNode->node->y - currentNode->node->y);
gcost = 0;
if (ydiff > 0 && xdiff > 0)
gcost = (int)((double)(xdiff + ydiff) / 1.4); // 1.4 is rough diagonal length of a square
else
gcost = xdiff + ydiff; // length of one side
cNode->node->gCost = gcost;
}
if (cNode->node->hCost == 0) // h cost
{
// this is the difference between the oNode and the destination node
xdiff = cNode->node->x - endNode->node->x;
ydiff = cNode->node->y - endNode->node->y;
hcost = (int)std::sqrt((double)(std::powf(xdiff, 2) + std::powf(ydiff, 2)));
cNode->node->hCost = hcost;
}
if (cNode->node->fCost == 0)
{
// this is the gcost and the hcost combined
cNode->node->fCost = (cNode->node->gCost + cNode->node->hCost);
}
// if the connected node is not within an obstacle
if (!cNode->node->isBlocked)
{
// if the connected node is not in the closed list
if (!cNode->node->closed)
{
// if the connected node is not in the open list
if (!cNode->node->opened)
{
cNode->node->aStarParent = currentNode->node;
OpenList.push_back(cNode); // add it to the open list
cNode->node->opened = true;
}
else
{ // if it is already in the open list
// check to see if its current gcost is less than the new gcost of the parent and the old gcost
gcost = cNode->node->gCost + currentNode->node->gCost;
if (gcost < cNode->node->gCost)
{
// if so, make the current node its new parent and recalculate the gcost, and fcost
cNode->node->aStarParent = currentNode->node;
cNode->node->gCost = gcost;
cNode->node->fCost = (cNode->node->gCost + cNode->node->hCost);
}
}
} // end closed list check
} // end blocked nodes
}
// at this point the open list has been updated to reflect new parents and costs
// loop through the open list
GameObject* cheapOpenNode = NULL;
std::list<GameObject*>::iterator i;
for (i = OpenList.begin(); i != OpenList.end(); ++i)
{
// compare the openList nodes for the lowest F Cost
if (cheapOpenNode == NULL) // initialize our cheapest open node
{
cheapOpenNode = (*i);
continue;
}
if ((*i)->node->fCost < cheapOpenNode->node->fCost)
{
// we found a cheaper open list node
cheapOpenNode = (*i);
}
}
if (cheapOpenNode == NULL) // we have run out of options, no shortest path
{
resetNodes();
return std::vector<GameObject*>();
}
// now we have the node from the open list that has the cheapest f cost
// move it to the closed list and set it as the current node
ClosedList.push_back(cheapOpenNode);
cheapOpenNode->node->closed = true;
OpenList.remove(cheapOpenNode);
cheapOpenNode->node->opened = false;
currentNode = cheapOpenNode;
} // A* Complete
// we have found the end node
// Loop from the current/end node moving back through the parents until we reach the start node
// add those to the list and we have our path
bool moreParents = true;
GameObject* workingNode = currentNode;
while (moreParents)
{
if (workingNode->node->aStarParent == NULL)
{
path.push_back(workingNode);
moreParents = false;
}
else
{
path.push_back(workingNode);
workingNode = workingNode->node->aStarParent;
}
}
// before we end, reset all our costs and parents in our nodes
resetNodes();
return path;
}
// TODO: Optimize the reason for this existing
void resetNodes()
{
for(int i=0; i < gameObjects.size(); i++)
{
gameObjects[i].node->resetAstar();
}
}